What is The Time Value of Money?
Time Value of Money Definition
The idea that money available at the present time is worth more than the same amount in the future due to its potential earning capacity. This core principle of finance holds that, provided money can earn interest, any amount of money is worth more the sooner it is received.A dollar on hand today is worth more than a dollar to be received in the future because the dollar on hand today can be invested to earn interest to yield more than a dollar in the future. The Time Value of Money mathematics quantify the value of a dollar through time. This, of course, depends upon the rate of return or interest rate which can be earned on the investment.
The Time Value of Money has applications in many areas of Corporate Finance including Capital Budgeting, Bond Valuation, and Stock Valuation. For example, a bond typically pays interest periodically until maturity at which time the face value of the bond is also repaid. The value of the bond today, thus, depends upon what these future cash flows are worth in today's dollars.
The Time Value of Money concepts will be grouped into two areas: Future Value and Present Value. Future Value describes the process of finding what an investment today will grow to in the future. Present Value describes the process of determining what a cash flow to be received in the future is worth in today's dollars.
How to Calculate Time Value of Money
1.Choose an option. If you are choosing Option A, your future value will be $10,000 plus any interest acquired over the three years. The future value for Option B, on the other hand, would only be $10,000. So how can you calculate exactly how much more Option A is worth, compared to Option B? Let's take a look,by following given below solved examples..
2
If you chose Option A and invest the total amount at a simple annual rate of 4.5%,
the future value of your investment at the end of the first year is
$10,450, which of course is calculated by multiplying the principal
amount of $10,000 by the interest rate of 4.5% and then adding the
interest gained to the principal amount:
- Future value of investment at end of first year:
- = ($10,000 x 0.045) + $10,000
- = $10,450
- = ($10,000 x 0.045) + $10,000
3
You can also calculate the total amount of a one-year investment with a simple manipulation of the above equation:
- Original equation: ($10,000 x 0.045) + $10,000 = $10,450
- Manipulation: $10,000 x [(1 x 0.045) + 1] = $10,450
- Final equation: $10,000 x (0.045 + 1) = $10,450
- Manipulation: $10,000 x [(1 x 0.045) + 1] = $10,450
4
The manipulated equation
above is simply a removal of the like-variable $10,000 (the principal
amount) by dividing the entire original equation by $10,000.
5If the $10,450 left in your investment account at the end of the first year is left untouched and you invested it at 4.5%
for another year, how much would you have? To calculate this, you would
take the $10,450 and multiply it again by 1.045 (0.045 +1). At the end
of two years, you would have $10,920:
- Future value of investment at end of second year:
- = $10,450 x (1+0.045)
- = $10,920.25
- = $10,450 x (1+0.045)
6
The above calculation, then, is equivalent to the following equation:
- Future Value = $10,000 x (1+0.045) x (1+0.045)
- After simplifying,we get Future Value = $10,920.25
- We can see that the exponent is equal to the number of years for which the money is earning interest in an investment.
- After simplifying,we get Future Value = $10,920.25
7
Future Value Calculator: So the above calculations and discussion shows that we
don't need to calculate the future value after the first year, then the
second year, then the third year, and so on. If you know how many years
you would like to hold a present amount of money in an investment, the
future value of that amount is calculated by the following equation:
8
Present Value Calculator Basics.The
current worth of a future sum of money or stream of cash flows given a
specified rate of return. Future cash flows are discounted at the
discount rate, and the higher the discount rate, the lower the present
value of the future cash flows. Determining the appropriate discount
rate is the key to properly valuing future cash flows, whether they be
earnings or obligations... To find the present value of the future
$10,000, we need to find out how much we would have to invest today in
order to receive that $10,000 in the future.
9
Time Value of Money Formula
10
Present Value of a Future Payment.The present value formula is the
core formula for the time value of money; each of the other formulae is
derived from this formula.
- Say you could receive either $15,000 today or $18,000 in four years. Which would you choose? let's find the present value of $18,000 if interest rates are currently 4%.

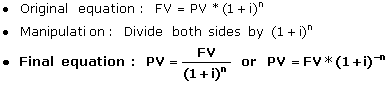





0 comments:
Post a Comment